A public service announcement from our good friends at the FBI, warns that motor vehicles are increasingly vulnerable to remote exploits, which in the wake of the bad-ass research from Chris Valasek and Charlie Miller shouldn’t be shocking.

What struck me, is that the security advice the FBI is offering drivers was identical to the advice cybersecurity experts have been giving to–well just about everyone. As more of your car intertwines with software to provide things like automatic wipers, ABS and even bluetooth audio, the more it becomes susceptible to cyber attacks we traditionally associated with software on servers rather four-wheeled auto-mobiles.

You don’t have a right to freedom of speech.

Obviously true if you’re Malaysian, but even Americans only enjoy a liberty in freedom of speech and not an absolute right.

The difference is clear, liberties are protections you have from the government, while rights are something you have from everyone.

So if someone threatened your right to live, the government is obligated to intervene and protect that right, because your right to live is a protection you have from everyone, whether it be a common criminal, abusive husband or Ayotollah Khomeini.

On the other hand you only have a liberty in freedom of speech (at least in an American context), which means that the government can’t prevent you from speaking, or penalize you for something you said.

However, the government is under no obligation to ensure your speech gets equal ‘air-time’, a newspaper may decline to publish your article, an auditorium may elect to deny you their roster, and online platforms like Facebook may choose to remove your post–all of which do not violate your freedom of speech, because freedom of speech is protection only from the government (state actors) and not from private entities.

And like all liberties and rights, freedom speech is not absolute. Under strict conditions even the US government can impose limits to what they’re citizens can say, or penalize them for things they have said.

In the case of freedom of speech, a liberty defined in their first amendment, those strict conditions are very strict indeed. In order for the government to infringe on the freedom of speech, it must demonstrate a imminent danger that will result in a serious effect.

In other words the government must be able to prove that if the speech were given freedom, there would be an imminent threat of something serious. Both the imminence and seriousness must be proven, failing which the government cannot infringe on that speech. This is indeed a very tall hurdle to climb, and based on my cursory research no case has ever reached this limit.

The Apple vs. FBI story has evolved so much in the past weeks, I thought I needed to write a separate post just on the updates. Admittedly, the story is far more complex and nuanced that I initially presumed, and everyone wants to be part of the conversation.

On one side, we have the silicon valley tech geeks, who seem to be unanimously in the corner of Tim Cook and Apple, while on the other  we have the Washington D.C policy makers, who are equally supportive of James Comey and the FBI whom he directs.

But to understand this issue from a fair and balanced perspective, we need to frame the correct question, not just what the issue about, but who is the  issue really focused on.

This isn't just about the FBI or Apple

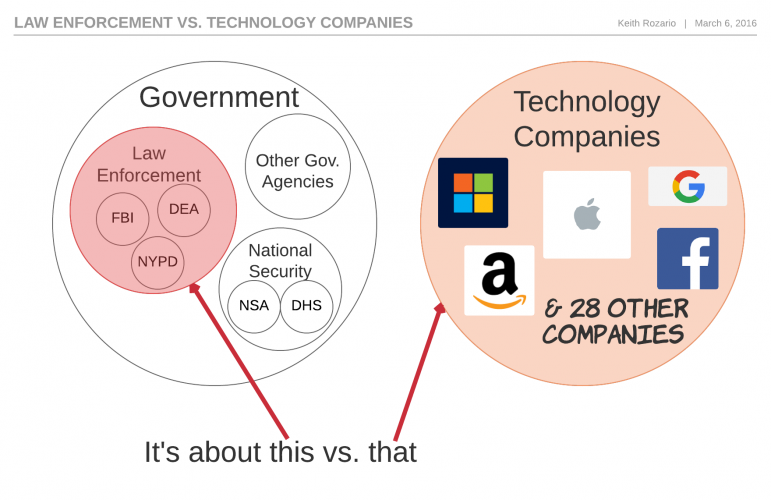
The FBI is just a part of the The Government, specifically the part tasked with investigating federal crimes.James Comey, FBI director, is genuinely trying to do his job when he uses the All Writs Act to compel Apple to create a version of iOS that would allow them to brute-force the PIN code.

But there are other parts of The Government, like the NSA, who have the wholly different task of national security. To them, if a smartphone, is genuinely secured from FBI, then it’s secured from Russian Cybercriminals and Chinese State Sponsored actors too (probably!).

And because so much data are on smartphones, including the smartphones of federal government employees, the national security interest of America is better protected by having phones that are completely unbreakable, rather than ones the provide exceptional access to law-enforcement. Exceptional being defined as, no one has access except for law enforcement, and perhaps TSA agents, maybe border patrol and coast guard–you can see how slippery a slope ’exceptional’ can be. Oh and by the way, exceptional doesn’t exist in end-to-end encryption.

Former NSA director, Michael Hayden, has openly said “I disagree with Jim Comey. I actually think end-to-end encryption is good for America”. So it appears the NSA has an interest of national security that competes with the FBIs interest of investigating crimes.

The Government isn’t a single entity with just one interest, rather it is a collection of agencies with sometimes competing objectives, even though they all ultimately serve their citizens.  Experts believe the NSA has the capability to crack the iPhone encryption easily, but are refusing to indulge the FBI, because–well it’s hard to guess why the NSA don’t like the FBI.

testimony to House Judiciary Committee. Both methods involved complicated forensics tools, but would cost a few hundred thousand dollars (cheap!) , and wouldn’t require Apple to write a weakened version of iOS. If the goverment can get into the phone for $100,000 , that would mean it couldn’t compel Apple under the All Writs Act (AWA).

Remember, the FBI buy their spyware from the lowlifes at hacking team, which means they’re about as competent as the MACC and Malaysian PMO, but if Comey and Co. can afford $775,000 on shit from Hacking Team, I’m guessing $100,000 for a proper computer forensics expert isn’t a problem.

But maybe there’s an ulterior motive here, at the very recently concluded Brooklyn iPhone case, Magistrate Judge Orenstein noted that necessity was a pre-requisite for any request made under AWA, and if the FBI have an alternative for a reasonable price, then Apple’s support was not necessary, and hence outside the ambit of the AWA. So maybe the NSA isn’t providing the support to necessitate the NSA.

An this isn’t singularly about the FBI either. The New York A-G is waiting for this case to set precedent before he makes request for the 175 iPhones he’s hoping to unlock for cases that aren’t related to terrorism or ISIS. You can bet he’s not the only A-G waiting for the outcome, and it’s highly unlikely for the Judge to make her ruling so specific that nobody except the FBI could use it as precedent.

But it’s also not just about Apple. The legal precedent set by this case would apply not just to every other iPhone, but possibly every other smartphone, laptop, car or anything else we could squeeze into the definition of a computer. This is about more than Apple, and that’s why the tech companies are lining up in support of Mr. Cook, 32  such companies the last I checked.

But now that we’ve framed the ‘who’ , let’s frame the ‘what’.

Imagine a small village of a 100 people.

One day,  a sorcerer shows up,  and grants all the villagers magical 1000-sided dice, which are purely random and can only be thrown at a fixed rate of 1 throw per second (no faster & no slower).

Over the next year, at noon of every day, the sorcerer will announce a random number between 1 and 1000, and the first villager to throw that number on their magical dice will earn $100, just by raising than hands and announcing it to the wizard.

The villagers play along, and the since the dice are purely random, each villager can expect to win $100 every 100 days.

But if they pooled their dice together they could create interesting scenarios. For example, a group of 10 ‘pooled’ villagers, could expect to win once every 10 days, and the winnings of $100 could be equally divided between them. To these villagers $10 every 10 days is a better deal than $100 every 100 days.

Eventually the village ends up with 2 pools of 50 villagers each. The pools expect to win once every other day, and the winnings would be $2 dollars per villager. So effectively, they’re winning $2 every 2 days.

So far so good.

The Crooked Pool attacks

However, one of these pools (called the crooked pool), starts to act all dick-dastardly. They send 25 of their members to infiltrate the other ‘honest’ pool. These infiltrators will roll their dice, but never claim announce their winnings to the sorcerer, even if they roll the magical number. Essentially these infiltrators become dead-weight on the honest pool, rolling dice choosing to never win. The remaining 25 members in the crooked pool will continue rolling and trying to win.

At first this seems illogical, why would a pool intentionally give up half it’s resources to sabotage another? How could discarding winnings actually benefit anyone? Does it even profit the crooks?

Yes it does:

• The crooked pool now has 25 villagers rolling dice;
• The honest pool has 75 villagers, but only 50 of them are effectively trying to win
• Don't forget, the crooked pool has 25 members in the honest pool, and hence is entitled to 1/3rd of their winnings.
• Which means the original 50 villagers in the honest pool, only get 2/3rd of their winnings.
• With only 75 villagers effectively throwing the dice, the crooked pool now has both it's original 25 members and a 1/3rd share of the remaining 50.
• The maths is only a 'bit' complicated, but the result is the crooked pool increases its chances of winning from 50% to 56%.

This isn’t just a thought experiment either, this is a problem known in bitcoin as the miners delimma, analogous to famous prisoner dilemma thought in game theory. Bitcoin mining works almost exactly like this scenario, it is a purely random function similar to dice throwing, whose odds of success can only be increased if you ramp up the hashing power, or in this case, adding villagers to a pool.

A judge in the US has ordered Apple to provide ’technical assistance’ to FBI, in creating what some (but not all) cybersecurity experts call a backdoor. In the few years I’ve written about these issues, I’ve never seen anything as hotly debated as this one, across the folks from digital security to foreign policy all coming down on both sides of the debate.

On one hand it seems a bit snarky of the FBI to use this one particular case, that looks to have the highest possible chance of success to set precedent, but on the other hand it seems mighty nasty of Apple to refuse to comply with a court order, to crack into a terrorist phone.

So here’s some facts of the case.

The phone in question belonged to Syed Rizwan Farook, a shooter in the San Bernadino shooting, which caused the deaths of 14 people. America has numerous mass shootings, but this one involved two Muslims aligned to ISIS–and hence more easily labeled terrorism, without the need for adjectives like ‘domestic’.

As I blogged about last week, self-radicalized terrorist don’t get funding from headquarters, and without that glorious ISIS-oil money, all these guys could afford for was an iPhone 5C, an entry-level phone with hardware identical to that of the iPhone 5, a phone launched waaaayy back in 2012 (you’ll remember that as the year Manchester United last won the Premier League). As an older phone, the security architecture of the 5C lagged behind the current generation iPhones, all of which have a secure enclave, but make no mistake, it’s still pretty secure.

By pretty secure, I mean that the phone has all of its contents encrypted, and un-readable to anyone without the encryption key. The key is derived from both the user passcode, and a randomly generated hardware key that is unique to the specific iPhone. It is generally understood that Apple doesn’t keep track of the hardware key, and therefore unable to provide it, as you might expect the hardware will also never give up it’s key under any circumstance. Without the hardware key, the encrypted  data is unreadable, even with the passcode. Which explains why the FBI can’t suck the data out of the device for decryption on a more powerful computer, or load the data into 1000’s of iPhones for parallel cracking.

Under the current hype of the FBI ordering Apple to ‘install backdoors’ on their iPhones, a bit of interesting news seems to have slid under the radar.

A court in Singapore ruled that e-mails from the Hacking Team breach, published by the hacker Phineas Fisher via a torrent download, and available freely on Wikileaks–were still confidential in nature.

The news hits close to home, after all, I’ve written a 2,000 word article on it back in July, and have been harping on the issue over the past weeks, even going on BFM radio for an interview.

So was I using confidential information in my tech evangelism?!

Well, probably not, but this does raise some interesting questions.

Here’s the facts of the case.

Today, I was on BFM talking about Hacking Team, the audio for which is below, and more comments and thoughts below that.

This is my last ditch attempt to get a conversation started about the use of surveillance software by the Government—and these conversations should take place a the higher (and more powerful) levels of goverment. Talking about it to myself on this blog isn’t taking it anywhere.

Our spanking new, hand-picked Attorney-General is proposing life imprisonment for journalist who refuse to reveal their sources.

And surprisingly, my favorite Member of Parliament,Dato Azalina Othman, has supported the move, saying it was ‘high-time’ Malaysian did something. Fortunately, some calmer more rationale heads, like Dato Paul Low have criticized the A-G for his short-sighted stupidity.

Putting aside the fact that anonymity of sources is a core component of Press freedom, it’s easy to extrapolate how harsher punishment for journalists who keep their sources anonymous will back-fire spectacularly for the Government.

If sources know that Journalist will be pressured to reveal their identities, most sources will stop speaking journalist, thereby stemming the leakages from the government, and keeping the status quo.Or so the theory goes…

Next week, I’ll be on BFM for an interview about spyware, which will be my last Hail Mary play to get a conversation started about the use of surveillance software by the Government. If a radio interview on a popular station won’t do it, nothing on my blog will possibly be able to anyway :)

In any case, this post is a pre-emptive response to a slightly controversial idea that I cover (very briefly) in the interview, and hopefully it can be articulated better here than in a radio segment. To be honest, I haven’t fully thought this through, but I believe it at least some some aspects of truth that deserve further attention.

The Idea comes in 3 parts:

1. Terrorism has changed dramatically with ISIS (or Daesh)
2. Our conventional approach to surveillance will be ineffective against this new threat
3. Our surveillance-based response to the new threat may end up hurting us more than ISIS ever could

Malaysian rejoiced last month when Netflix announced that they would be coming to our shores. We were all salivating over the massive amount of content we would finally have access too…except that it wasn’t so massive.

Malaysia would enjoy less than 20% of what was available to Netflix users in the US or even in the UK, and that looked like an especially lousy deal since we were paying the same amount for our subscriptions.

I wasn’t that interested in the news, after all, I had already subscribed to Netflix for more than 2 years, and used a VPN to enjoy US and even UK content. I loved Netflix because it had a lot of interesting content, but what really sealed the deal for me was Pocoyo and Dora the explorer…I’m a father of a 2-year-old, and having a video on demand service that lets me address my toddlers demand was a life-saver.

Netflix was far more effective than youtube for videos for my kid, first of all, the content was pure, and I could be sure that nobody was messing with it or adding commentary, but more importantly, it had no adverts, and when you have a 2-year-old the last thing you want them to watch is adverts.