I remember this problem from watching an episode of numbers. You’re a contestant on a game show–and you’re given 3 doors to choose from.
Behind one door is a shiny new sports car–behind the other 2 are goats. Your goal is to get the sportscar, by choosing a door. But after you choose a door the host reveals one of doors with the goats. Leaving you with you just two doors, instead of your initial 3.
The choice is now yours again–do you switch doors or do you keep your initial choice–or do you think it doesn’t matter.
Think about it.
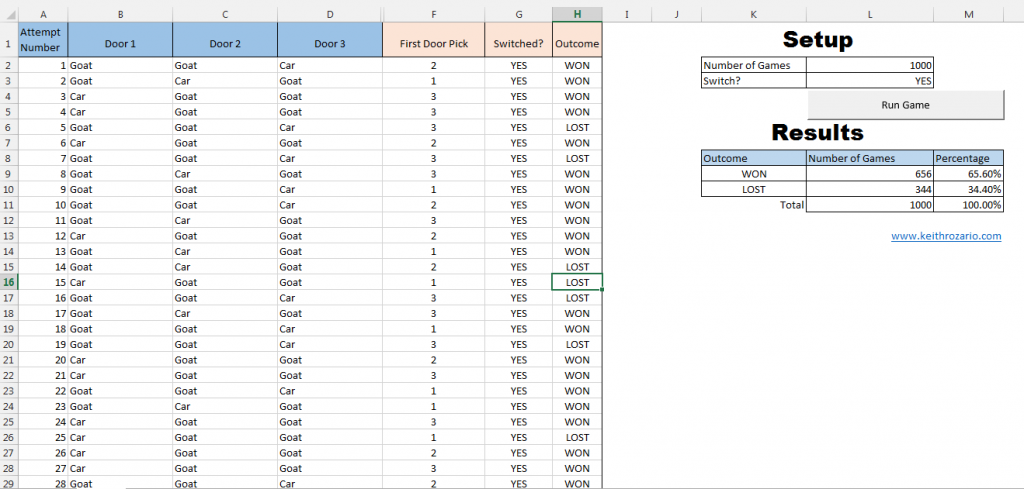
The answer is that’s is always better to switch, in fact your two times more likely to win the car if you switch than if you don’t. There’s a quick video at the bottom of the post, outlining the problem, but here’s an excel spreadsheet simulation I coded with some macros to help you visualize the problem.
All you have to do is enter in how many games you want to play (the default is 1000), and what kind of switching you want:
- YES – Switches the choice everytime
- NO – keeps the initial choice door everytime
- RANDOM – randomly selects a door from the remaining 2 doors
Then you can see how many games you would have lost or won based on your strategy, and it’s clear that switching is twice more successful than keeping. To download the spreadsheet click here.
One way to think of it, is that your initial choice has a 1/3 chance of winning the car. Meaning you had a 2/3 chance of losing. So your initial choice was most likely wrong, and switching after the a goat is revealed flips your chances of winning from 1/3 to 2/3.
[…] Which door should you choose? Will you win the car or a goat? Keith Rozario tests the Monty Hall problem in Excel. […]
There is no ‘Problem’ The Monty Hall statistical analysis is rubbish. First, Monty has to open an empty door.
Then 3 closed doors probability 1/3. 2 closed doors probability 1/2. All other explanations and analyses are illogical if not stupid.